

My name is Christophe Wacheux. I am a french researcher in mathematics. After a post-doc in mathematics at the École Polytechnique Fédérale de Lausanne (CH), a "Teaching Assistant" position at University of Manchester and another postdoc at the IBS Center of Geometry and Physics in South Korea, i decided to shift my career towards environmental engineering. Can't wait for tomorrow to do what we can.
This is my professional webpage. Please feel free to take a look and contact me.
Christophe Wacheux
UPCOMING EVENTS
FDIS 2017
from 3rd to 7th of July 2017
IBS-CGP & BICMR Joint Symplectic Workshop
from 31st of October to 4 of November 2016
You can find HERE the Beamer of my talk and photos of my and . The videos should be available on the website.
CSF Ascona - Integrable systems 2016
from 20th to 24th of June 2016
You can find HERE the abstract for the talk I will give at the conference.
Poisson 2016 - Poisson Geometry in Mathematics and Physics
Summer school from June 27 to July 2 2016
Conference from July 4th to July 8th, 2016
TTT100: Topology Transpennine Triangle
from 6th to 7th of September, 2016
MY LATEST RESEARCH
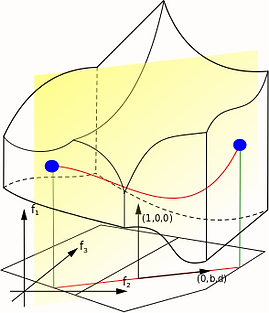
For a toric integrable Hamiltonian system (IHS) with n degrees of freedom, the image of the moment map F is a n-dimensional rational convex polytope.
This is no longer the case when we deal with semi-toric IHS. Yet we can recover a nice description of the image of the moment map for these systems. This requires a good description of the loci of semi-toric critical values.

In semi-toric systems, because of singularities with "focus-focus" components, the Lagrangian foliation degenerates as pinched tori appear. Of course, since the leaf is not regular, we cannot apply Arnol'd-Liouville theorem, but a singular form of it (this theorem is due to N.T. Zung), which gives us an incomplete set of Action-Angle coordinates.
However, it is still possible to give complete Action-Angle coordinates on every regular leaf near the focus-focus one. In a recent paper that has been accepted for publication, I analyze the asymptotic behaviour of these coordinates to understand the degeneration of the foliation.
