Asymptotics of Action variables near semi-toric singularities

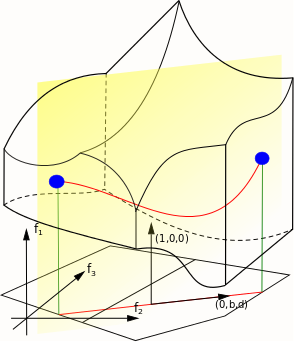
Near singularities with focus-focus components, the Lagrangian torus foliation given by a semi-toric integrable Hamiltonian system is pinched. At the critical leaf, one can't define a complete set of Action-Angle variables. For the Action-angles coordinates defined around it, there is a divergence of action variables, and a monodromy phenomenon.

In our paper, we show that both these two phenomenon comes from a complex logarithmic term in Action-Angle variable when defined around a focus-focus singularity. Once removed, the regularized action is an invariant of the system that describe the pinching of the foliation. We also compute the monodromy matrix.