Given a Hamiltonian action of a k-torus T on a symplectic manifold M of dimension 2n with moment map J:M --> R^k, a theorem discovered by Atiyah, and by Guillemin & Sternberg independently, states that
AGS-1°) The fibers of J are connected,
AGS-2°) The image of the moment map is a rational, convex polytope.
Note that only Atiyah actually mentioned the connectedness of the fibres in his article. Delzant used this theorem in the case of the so-called "toric integrable system" (k=n) to prove that
D-1°) The image of the moment map is Delzant: that is, it is rational convex and normal (i.e. from all its vertices, J(M) generates a basis for the n-dimensional lattice),
D-2°) Two toric systems are the same up to a T-equivariant symplectomorphism if and only if their image of the moment map are the same.
D-3°) Given a Delzant polytope, one can construct a (unique) smooth manifold, a symplectic form on it and a toric system on it such that its image is the given Delzant polytope.
The Delzant polytope is all the more convenient because one can read the dynamics of the integrable system on it very easily.
The toric systems can be seen from two angles: as the integrable case for AGS theorem, or as a particular case of an integrable system. From this come the generalization of toric systems known as "semi-toric systems".
They are integrable systems F=(H,J) on a (compact, connected) 2n-dimensional manifold such that:
- all points are such that, there exists suitable "symplectic local coordinates" (x_1,y_1,...,x_n,y_n) called Darboux coordinates, in which F=A o (q_1,..,q_n) + o(2) with A an invertible matrix, and q_i of the form:
- Elliptic: q_i = (x_i)² + (y_i)²
- Focus-focus :
| q_i = x_i y_i + x_{i+1} y_{i+1}
| q_{i+1} = x_i y_{i+1} + x_{i+1} y_i
- Transverse : q_i = y_i
- J gives a Hamiltonian (n-1)-torus action
The next question, if one want to extend the theory to the semi-toric case, is to look what remains of AGS theorem. While clearly one can still apply AGS theorem to J, we cannot do the same for F. Indeed, if there is a Focus-focus component at a critical point, the "q_i" in the local model makes it impossible to have an extra S^1 action with H.
An AGS theorem and a Delzant-like classification were done by Vu Ngoc and Pelayo. I managed to prove several theorems in my thesis and after that provide a "semi-toric version" of the AGS theorem. I show that, under mild assumptions
W - 1°) there is a stratification, or more precisely, a skeletization of semi-toric systems by smaller semi-toric systems: a semi-toric system is made of semi-toric systems over symplectic submanifolds P_k that are "patched together",
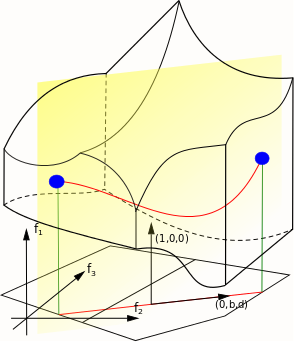
W - 2°) from this, one can deduce what J(M) looks like, by describing the image of the moment map for each strata. There are two cases depending on the relative value of rank(F) and rank(J) at the strata: either the image is the graph of function, or the intersection between the (strict) epigrahs and the hypograph of two different functions,
W - 3°) using the two previous results, I prove that the fibres are again connected.
While there is more information necessary to describe the dynamics of the system, if we know where the rank of F drops, one can use F(M) to get the same kind of information as in the toric case. This generalizes to any dimension the results obtained by Vu Ngoc in dimension 2n=4.
This result is, in turn, very interesting in the perspective of extending the classification of semi-toric systems to any dimension.
The first two results are in my thesis but will be published in an extended (and hopefully, simpler) version (a first version that uses local models is already available on Arxiv). The connectedness of the fibres is proven in my thesis provided that 1°) and 2°) are true. I expect to publish this result on a separate paper.