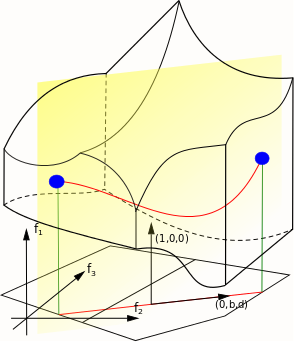
As we said in the previous post, for a semi-toric system the image of the moment map is the intersection between the epigraph and the hypograph of two piecewise-smooth functions over a polytope. Thus it is not a convex subset of R^n in general.
However, if we take a more "intrinsic" point of view, we can look at the base space of the Lagrangian foliation associated to the semi-toric system. The celebrated Arnold-Liouville-Mineur theorem of Action-Angle coordinates equips this base space with an integral affine structure, for which one can define a notion of "intrinsic convexity", at least on the regular points.
Together with Tudor Ratiu and Nguyen Tien Zung, we give a definition of convexity in a singular setting. We then proved that the base space of a semi-toric system in any dimension is convex, along with several other results concerning more general classes of Lagrangian fibrations.
We also came up with interesting counter-example of what can go wrong at each step (local and global), in order to prove a convexity result. In particular, we came up with an example of an almost-toric Lagrangian fibration (a Lagrangian fibration that looks locally like an semi-toric system) that is locally convex but not globally convex ! In this exaple, the base space is a sphere with 24 punctures corresponding to the focus-focus singularities, and the total space is diffeomorphic to a K3 surface. I'll give details in another post.